7. Probabilidades en estado estable

En este capítulo se presenta la definición, cálculo y uso de las probabilidades en estado estable. Tanto para cadenas de Markov de tiempo continuo como para cadenas de Markov de tiempo discreto, se presentarán ejemplos prácticos y usos frecuentes de estas probabilidades.

7.1. Introducción

Un sistema, al momento de ser observado por primera vez, está en sus condiciones iniciales. Por ejemplo, un banco vacío cuando abre, una planta de producción recibiendo las órdenes a producir durante el día o un call center donde los trabajadores están esperando las llamadas. A partir del estado inicial, un sistema evoluciona en el tiempo, y puede llegar a alcanzar una condición denominada estabilidad o estado estacionario (en inglés, steady-state o stationary state).

Los modelos de cadena de Markov (en tiempo discreto o continuo) pueden igualmente evolucionar en el tiempo hasta alcanzar el estado estacionario. Es posible demostrar que la propiedad de ergodicidad es suficiente para que una cadena de Markov tenga estado estable.

Hasta que una cadena de Markov no llegue a un punto en donde esté en condiciones de estabilidad, su comportamiento es de tipo transitorio y debe ser analizado utilizando las técnicas del análisis transitorio. El tiempo que se demora para llegar a esta estabilidad se conoce como tiempo de calentamiento, y cada sistema/modelo tiene un tiempo de calentamiento diferente. Por ejemplo, el número promedio de personas en un banco puede tener el siguiente comportamiento:

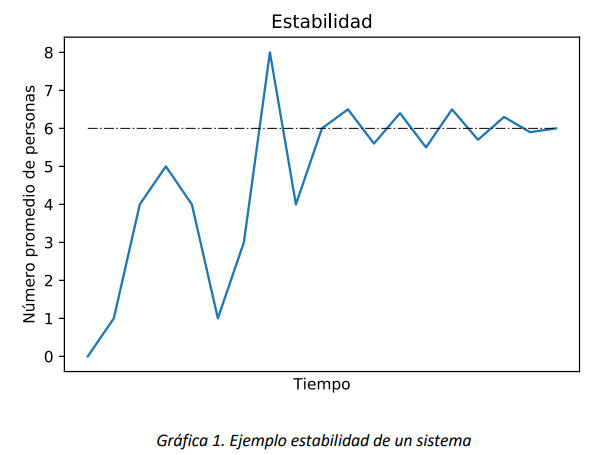
Se puede apreciar que el número de personas se estabiliza alrededor del valor de 6 personas en el banco. Desde este punto se determina la estabilidad. Ahora bien, como cada sistema se comporta de forma diferente se puede concluir que, para el modelo de un sistema que admita estado estable, cuando el tiempo tiende a infinito el modelo llega seguramente a una estabilidad.

En particular, si una cadena de Markov con espacio de estados \(S\) admite estado estable, se observa que, en el largo plazo, cuando el tiempo (discreto o continuo) tiende al infinito, existen los siguientes límites:

\(\lim_{t \rightarrow \infty}{P\left\lbrack X(t) = j \middle| X(0) = i \right\rbrack = \pi_{j}\ ,\ \forall\ i,j \in S}\) si la cadena es continua

\(\lim_{n \rightarrow \infty}{P\left\lbrack X_{n} = j \middle| X_{0} = i \right\rbrack = \pi_{j}\ ,\ \forall\ i,j \in S}\) si la cadena es discreta

Observamos que no solo los límites \(\pi_{j}\) existen por cada estado, sino que son independientes del estado inicial de la cadena de Markov. Esta independencia del estado inicial resulta de la ergodicidad del modelo, en particular de la irreducibilidad. Cuando una cadena es ergódica, las probabilidades límite \(\pi_{j}\), \(j \in S\), son equivalentes a las probabilidades de estado estable, y el vector \(\overrightarrow{\pi}\) de las probabilidades de estado estable es el vector de distribución estacionaria de estado (steady-state probability distribution vector, en inglés). Al ser un vector de probabilidades, la suma de los elementos de \(\overrightarrow{\pi}\) tiene que ser unitaria, es decir:

\[\sum_{i \in S}^{}\pi_{i} = 1\]

7.2. Cálculo de las probabilidades en estado estable para CMTD

Para una cadena de Markov de tiempo discreto se puede calcular las probabilidades en estado estable conociendo que:

\[\lim_{n \rightarrow \infty}P\left\lbrack X_{n} = j \middle| X_{0} = i \right\rbrack = \lim_{n \rightarrow \infty}\mathbb{P}_{ij}^{n}\]

Pero esto quiere decir que se debería elevar la matriz \(\mathbb{P\ }\)al infinito, o, si se acepta una aproximación, por lo menos calcular una potencia muy grande de \(\mathbb{P}\). Dado que este cálculo puede ser muy costoso en términos computacionales, es necesario utilizar otro procedimiento. La siguiente propiedad de las CMTD proporciona una manera más efectiva de calcular la distribución de estado estable.

7.2.1. Propiedad:

Para una CMTD \(\{ X_{n},n \geq 0\}\) ergódica, con espacio de estados \(S\) y matriz de probabilidades de transición a un paso \(\mathbb{P}\), las probabilidades en estado estable son calculadas resolviendo el siguiente sistema de ecuaciones:

1. \(\overrightarrow{\pi}\mathbb{P =}\overrightarrow{\pi}\) (Ecuaciones de balance)

2. \(\sum_{i \in S}^{}\pi_{i} = 1\) (Ecuación de normalización)

La primera expresión se puede interpretar así: Si una cadena se encuentra en estado estable, es decir, si la cadena se encuentra en el estado \(i\) con probabilidad \(\pi_{i}\) para todo \(i \in S\), tras una transición de acuerdo con la matriz \(\mathbb{P}\), la cadena seguirá en cada estado con la misma probabilidad, i.e., en cada estado \(i \in S\) estará con probabilidad \(\pi_{i}\). La segunda afirmación hace referencia al hecho de que \(\overrightarrow{\pi}\) es un vector estocástico, y por ende la suma de todos sus elementos debe ser igual a uno. Adicionalmente, cabe resaltar que existen tantas ecuaciones de balance como estados en la cadena, \(n = \ |S|\), y que estas son linealmente dependientes entre si (el sistema tiene infinitas soluciones). Por esta razón, a la hora de calcular las probabilidades se deben usar \(n - 1\) ecuaciones de balance, más la ecuación de normalización.

Ejemplo

Una tienda de televisores tiene una capacidad para mantener en inventario máximo 3 unidades. Si al final de la semana (domingo) no tiene televisores en inventario, se piden nuevas unidades hasta llenar el inventario. Este pedido llega al principio de la semana siguiente (lunes) a primera hora.

Se sabe que la demanda de televisores por semana se comporta de la siguiente forma: 0 televisores con probabilidad de \(\frac{1}{4}\), 1 televisor con probabilidad de \(\frac{1}{2}\) y 2 televisores con probabilidad de \(\frac{1}{4}\). Si la demanda no puede ser abastecida en una semana, aun así, vende la mayor cantidad de televisores posibles. Determine las probabilidades en estado estable del inventario.

Solución Ejemplo

Se define la variable como \(X_{n} = El\ número\ de\ televisores\ en\ inventario\ al\ principio\ de\ la\ n - \text{ésima semana}\). Por lo que el espacio de estados es \(S = \{ 1,2,3\}\). Este no contiene el 0, dado que, al definir el periodo de observación de la variable al inicio de la semana, si el domingo no hay unidades en el inventario, se pedirán 3 unidades hasta saturar el sistema. En caso que haya una o más unidades en inventario al final de la semana (domingo), no se pedirán unidades. Esto muestra que, de acuerdo con la definición de la temporalidad de \(X_{n}\), el estado \(X_{n} = 0\) nunca se observará.

Warning

Nota: Considere que, si la definición de la variable cambia, y ahora se observara al final de la semana, sería posible observar el estado \(X_{n} = 0\). Reflexione sobre cómo cambiaría la matriz de probabilidades con esta nueva variable.

Por ejemplo, si el domingo se finalizara con una unidad, no se realizaría ningún pedido, y se iniciaría el lunes \(n\) con dicha unidad. Para que el siguiente lunes \((n + 1)\) siga existiendo una unidad en inventario, en la semana no se debe demandar ninguna unidad, lo cual sucede con probabilidad de \(\frac{1}{4}\). Adicionalmente, la transición de tener 1 unidad en el inventario y pasar a 3 unidades requiere que la demanda en la semana haya sido de 1 o más unidades, lo que lleva a tener cero unidades en el inventario, y realizar el pedido el día domingo. Lo anterior se puede resumir como: \(p_{1,1} = \frac{1}{4},\ \) y \(p_{1,3} = \frac{3}{4}\).

Siguiendo la misma lógica para el resto de los casos, se tiene entonces que la matriz de probabilidades de transición está expresada por:

\[\begin{split}\mathbb{P = \ }\begin{matrix} \ & \begin{matrix} 1\ \ & \ 2\ & \ \ 3 \end{matrix} \\ \begin{matrix} 1 \\ 2 \\ 3 \end{matrix} & \begin{bmatrix} 1/4 & 0 & 3/4 \\ 1/2 & 1/4 & 1/4 \\ 1/4 & 1/2 & 1/4 \end{bmatrix} \end{matrix}\end{split}\]

Para calcular las probabilidades en estado estable, primero hay que formular las ecuaciones de balance \(\left( \overrightarrow{\pi}\mathbb{P =}\overrightarrow{\pi} \right)\):

\[\begin{split}\overrightarrow{\pi}\mathbb{P =}\overrightarrow{\pi} = > \ \begin{bmatrix} \pi_{1} & \pi_{2} & \pi_{3} \end{bmatrix}\begin{bmatrix} 1/4 & 0 & 3/4 \\ 1/2 & 1/4 & 1/4 \\ 1/4 & 1/2 & 1/4 \end{bmatrix} = \begin{bmatrix} \pi_{1} & \pi_{2} & \pi_{3} \end{bmatrix}\end{split}\]

\[\frac{1}{4}\pi_{1} + \frac{1}{2}\pi_{2} + \frac{1}{4}\pi_{3} = \pi_{1}\]

\[0\pi_{1} + \frac{1}{4}\pi_{2} + \frac{1}{2}\pi_{3} = \pi_{2}\]

\[\frac{3}{4}\pi_{1} + \frac{1}{4}\pi_{2} + \frac{1}{4}\pi_{3} = \pi_{3}\]

Adicionalmente, se debe agregar la ecuación de normalización:

\[\pi_{1} + \pi_{2} + \pi_{3} = 1\]

Dado que las ecuaciones de balance son linealmente dependientes entre sí, se debe escoger 2 de estas ecuaciones más la de normalización para resolver el sistema. Al resolver el sistema de ecuaciones, las probabilidades en estado estable resultantes son:

\[\pi_{1} = \frac{7}{22},\ \pi_{2} = \frac{6}{22},\ \pi_{3} = \frac{9}{22} \]

El anterior resultado implica que, en estado estable, la probabilidad de que en una semana cualquiera se inicie con 1,2 y 3 televisores en inventario, es de \(\frac{7}{22}\), \(\frac{6}{22}\) y \(\frac{9}{22}\), respetivamente.

7.3. Probabilidades en estado estable para CMTC

Para una cadena de Markov de tiempo continuo, a diferencia de una de tiempo discreto, se cuenta con una matriz generadora conocida como \(\mathbb{Q}\). Para las CMTC, el cálculo de las probabilidades de estado estable se basa en la siguiente propiedad:

7.3.1. Propiedad:

Para una CMTC \(\{ X(t),t \geq 0\}\) ergódica, con espacio de estados \(S\) y matriz generadora \(\mathbb{Q}\), las probabilidades en estado estable son calculadas resolviendo el siguiente sistema de ecuaciones

1. \(\overrightarrow{\pi}\mathbb{Q =}\overrightarrow{0}\) (Ecuaciones de balance)

2. \(\sum_{i \in S}^{}\pi_{i} = 1\) (Ecuación de normalización)

En la primera expresión, considere la primera entrada del producto \(\overrightarrow{\pi}\mathbb{Q}\), que es el resultado de multiplicar el vector fila \(\overrightarrow{\pi}\) por la primera columna de \(\mathbb{Q}\). La primera columna contiene la tasa de salida del primer estado (negativa) y las tasas de entrada al primer estado desde cualquier otro estado. El producto de \(\overrightarrow{\pi}\) por la primera columna de \(\mathbb{Q}\) tiene entonces una suma positiva de tasas de entrada al primer estado, más la tasa de salida (negativa), ponderados por la probabilidad de estado estable asociada a cada estado. Si este producto es igual a cero, la tasa de salida es igual a la tasa entrada, y por lo tanto no se esperan cambios en la probabilidad. Así, la distribución de estado estable logra balancear las probabilidades para que las tasas de entrada y salida sean iguales en estado estable. La segunda condición captura que \(\overrightarrow{\pi}\) es un vector estocástico, luego sus entradas deben sumar uno.

Ejemplo

Un banco cuenta con dos cajeros donde cada uno tiene un tiempo de atención que se distribuye exponencial con tasa de 10 personas por hora. Por otro lado, llegan clientes al banco en promedio cada 12 minutos. Se conoce que el banco tiene espacio a lo sumo de 1 persona en fila y que el tiempo entre llegadas de clientes se distribuye exponencial. Determine las probabilidades en estado estable del número de personas en el banco.

Solución Ejemplo

Solución.

Se define la variable como \(X(t) = \ El\ número\ de\ personas\ en\ el\ banco\ en\ cualquier\ momento\ t\). Considerando que como máximo se pueden estar atendiendo dos personas, más la que se encuentra en la fila, el espacio de estados se define como \(S = \{ 0,1,2,3\}\). Ahora, aplicando el concepto de mínimo de exponenciales (visto en la lectura 2-Procesos de Poisson), y usando la tasa de llegada y la tasa de atención, se sabe entonces que la matriz generadora se puede representar como:

\[\begin{split}\mathbb{Q =}\begin{matrix} \ & \begin{matrix} 0 & \ \ \ 1\ \ & \ \ \begin{matrix} \ \ \ 2\ & \ \ \ 3 \end{matrix} \end{matrix} \\ \begin{matrix} 0 \\ 1 \\ \begin{matrix} 2 \\ 3 \end{matrix} \end{matrix} & \begin{bmatrix} - 5 & 5 & \begin{matrix} \ \ 0\ \ \ & 0 \end{matrix} \\ 10 & - 15 & \ \ \begin{matrix} 5\ \ \ & 0 \end{matrix} \\ \begin{matrix} 0 \\ 0 \end{matrix} & \begin{matrix} 20 \\ 0 \end{matrix} & \begin{matrix} \begin{matrix} - 25 \\ 20 \end{matrix} & \begin{matrix} 5 \\ - 20 \end{matrix} \end{matrix} \end{bmatrix} \end{matrix}\end{split}\]

Para calcular las probabilidades en estado estable, primero hay que formular las ecuaciones de balance \(\left( \overrightarrow{\pi}\mathbb{Q =}\overrightarrow{0} \right)\):

\[\begin{split}\overrightarrow{\pi}\mathbb{Q =}\overrightarrow{0} = > \begin{bmatrix} \begin{matrix} \pi_{0} & \pi_{1} \end{matrix} & \pi_{2} & \pi_{3} \end{bmatrix}\begin{bmatrix} - 5 & 5 & \begin{matrix} \ \ 0\ \ \ & 0 \end{matrix} \\ 10 & - 15 & \ \ \begin{matrix} 5\ \ \ & 0 \end{matrix} \\ \begin{matrix} 0 \\ 0 \end{matrix} & \begin{matrix} 20 \\ 0 \end{matrix} & \begin{matrix} \begin{matrix} - 25 \\ 20 \end{matrix} & \begin{matrix} 5 \\ - 20 \end{matrix} \end{matrix} \end{bmatrix} = \begin{bmatrix} \begin{matrix} 0 & 0 \end{matrix} & 0 & 0 \end{bmatrix}\end{split}\]

\[- 5\pi_{0} + 10\pi_{1} = 0\]

\[5\pi_{0} - 15\pi_{1} + 20\pi_{2} = 0\]

\[5\pi_{1} - 25\pi_{2} + 20\pi_{3} = 0\]

\[5\pi_{2} - 20\pi_{3} = 0\]

Aparte se debe agregar la ecuación de normalización:

\[\pi_{0} + \pi_{1} + \pi_{2} + \pi_{3} = 1\]

Dado que las ecuaciones de balance son linealmente dependientes entre sí, se debe escoger 3 de estas ecuaciones más la de normalización para resolver el sistema. Al resolver el sistema de ecuaciones, las probabilidades en estado estable resultantes son:

\[\pi_{0} = \frac{32}{53},\ \pi_{1} = \frac{16}{53},\ \pi_{2} = \frac{4}{53},\ \pi_{3} = \frac{1}{53}\]

Esto implica que, en el largo plazo, la probabilidad de que el banco se encuentre vacío en cualquier momento del tiempo es de \(\frac{32}{53}\), mientras la probabilidad de que haya 1 cliente es \(\frac{16}{53}\), 2 clientes \(\frac{4}{53}\), y finalmente 3 clientes \(\frac{1}{53}\).