Complementaria 1: Introducción a Python
#
Esta complementaria está diseñada para hacer una introducción a Python y aprender a definir y manejar matrices en Python. El uso de matrices aplicado a la construcción de Cadenas de Markov también será tratado a lo largo de la complementaria. Python es un lenguaje de programación de alto nivel, ampliamente utilizado por su simplicidad y legibilidad. En esta complementaria, cubriremos los fundamentos del lenguaje, incluyendo la sintaxis básica, la estructura de control de flujo, y las principales bibliotecas que hacen de Python una herramienta poderosa para una amplia gama de aplicaciones.
Para ejecutar Python utilizaremos Visual Studio Code (VSC), un editor de código fuente gratuito y multiplataforma desarrollado por Microsoft.
Asignación de variables
Las variables en Python se utilizan para almacenar datos que puedes usar más adelante en tu código. Puedes asignar valores a las variables utilizando el operador ‘=’.
nombre = 'Juan'
edad = 25
altura = 1.75
#Imprimir los valores de las variables.
print(nombre)
print(edad)
print(altura)
Juan
25
1.75
Tipos de objetos
En Python existen diferentes tipos de objetos para representar datos. Aqui se presenta una introducción a los tipos de objetos más comunes:
Cadenas de Texto (‘str’)
Listas (‘list’)
Tuplas (‘tuple’)
Diccionarios (‘dict’)
Booleanos (‘bool’)
Las cadenas de texto son secuencias de caracteres. Se pueden definir usando comillas simples (‘’) o dobles (“”)
nombre = 'Juan'
mensaje = "Hola ¿Cómo estás?"
Las listas son colecciones ordenadas y mutables de elementos. Los elementos pueden ser de diferentes tipos y se puede modificar la lista después de crearla.
frutas = ["manzana", "banana", "cereza"]
print(frutas)
['manzana', 'banana', 'cereza']
Para acceder a un elemento especifico de una lista lo podemos hacer por su posición. Recordemos que las posiciones en Python inician desde el 0. Así, si queremos acceder al segundo elemento de una lista, su posición correspondera a el numero 1
# Acceder a un elemento
print(frutas[1])
banana
También podemos añadir nuevos elementos a una lista.
# Añadir un nuevo elemento
frutas.append("naranja")
print(frutas)
['manzana', 'banana', 'cereza', 'naranja']
Las tuplas son colecciones ordenadas e inmutables de elementos. Una vez creada una tupla, no se puede modificar.
coordenadas = (10, 20)
print(coordenadas)
(10, 20)
De igual manera que con las listas, podemos acceder a un elemento especifico de la tupla sabiendo su posición recordando que las posiciones en Python empiezan desde 0.
# Acceder a un elemento
print(coordenadas[0])
10
Los diccionarios son colecciones no ordenadas de pares clave-valor. Se puede acceder a los valores usando las claves correspondientes.
persona = {
"nombre": "Samuel",
"edad": 24,
"ocupacion": "Ingeniero"
}
print(persona)
{'nombre': 'Samuel', 'edad': 24, 'ocupacion': 'Ingeniero'}
Para acceder a los valores de un diccionario se puede utilizar su respectiva clave:
# Acceder a un valor usando una clave
print(persona["edad"])
24
Los booleanos representan valores de verdad y solo pueden ser True o False.
es_mayor_de_edad = True
es_adolescente = False
Paquetes o librerias en Python
En Python los paquetes deben ser instalados cuando estos no están presentes en el computador, y también se deben cargar en cada sesión. Para instalar la librería jmarkov en la terminal puede emitir el comando
pip install jmarkov
O desde una celda de un cuaderno puede hacer con el siguiente comando, para eso se debe utilizar el siguiente comando:
!pip install jmarkov
Requirement already satisfied: jmarkov in c:\users\maria\appdata\local\programs\python\python311\lib\site-packages (0.3.2)
[notice] A new release of pip is available: 25.0 -> 25.2
[notice] To update, run: C:\Users\maria\AppData\Local\Programs\Python\Python311\python.exe -m pip install --upgrade pip
Requirement already satisfied: numpy in c:\users\maria\appdata\roaming\python\python311\site-packages (from jmarkov) (1.26.4)
Requirement already satisfied: scipy in c:\users\maria\appdata\roaming\python\python311\site-packages (from jmarkov) (1.15.2)
Requirement already satisfied: typing in c:\users\maria\appdata\local\programs\python\python311\lib\site-packages (from jmarkov) (3.7.4.3)
Una vez se ha instalado la librería, se puede importar toda su funcionalidad con el siguiente comando
import jmarkov #Importar la libreria
Funciones en Python
Para definir una función en Python, se utiliza la palabra clave def, seguida del nombre de la función y paréntesis que pueden contener parámetros opcionales. El bloque de código de la función está indentado. A continuación se presenta la sintaxis basica:
def nombre_de_la_funcion(parametros):
# Código de la función
return # Palabra clave para indicar qué debe retornar la función.
Ahora un ejemplo: Se quiere crear una función cuyo argumento es un número cualquiera y que devuelva la raíz cúbica del número que se ingresó por parámetro más 10. El código de la función tendrá la siguiente estructura:
def funcion2(n):
valor = ((n)**(1/3)) + 10
return valor
Una vez que se haya definido la función, se puede llamar utilizando su nombre seguido de paréntesis.
funcion2(4)
11.5874010519682
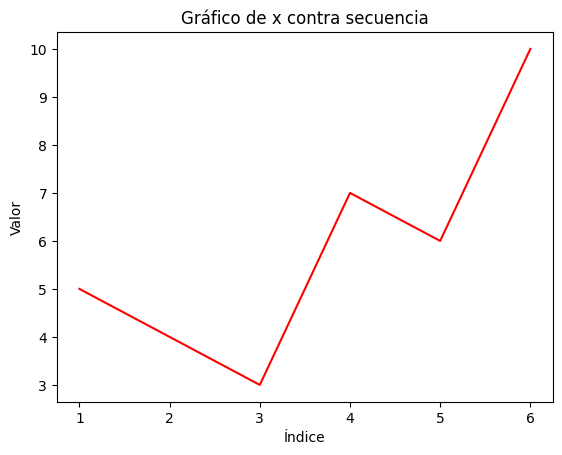
Las funciones no necesariamente deben retornar valores numéricos. Por ejemplo, en la siguiente función no se retornará nada y al llamarla se creará una gráfica.
import matplotlib.pyplot as plt # Libreria para crear el grafico
def funcion3(x):
y = list(range(1, len(x) + 1)) # Crear la secuencia de 1 a la longitud de x
plt.plot(y, x, color = 'red') # Graficar con líneas de color rojo
plt.xlabel('Índice') # Etiqueta del eje x
plt.ylabel('Valor') # Etiqueta del eje y
plt.title('Gráfico de x contra secuencia') # Título del gráfico
plt.show() # Mostrar el gráfico
# Vector de ejemplo
vector1 = [5, 4, 3, 7, 6, 10]
# Llamar a la función con el vector
funcion3(vector1)
Recorridos o ciclos
En algunas ocasiones, es necesario recorrer los elementos de otro elemento como son las listas o los diccionarios. Para hacerlo, en Python podemos utilizar los ciclos for de la siguiente manera:
for variable in secuencia:
# Código a ejecutar para cada elemento en la secuencia
Cell In[17], line 2
# Código a ejecutar para cada elemento en la secuencia
^
SyntaxError: incomplete input
Ejemplo: Se quiere crear una función cuyos parámetros sean dos listas (de cualquier tamaño) y esta función retorne una lista, donde cada posición de la lista resultante debe ser el máximo de las mismas posiciones entre las listas parámetro. La función funcion4 acepta exclusivamente dos listas de igual tamaño como argumentos. En el caso de que una lista sea mas corta que otra se producirá un IndexError.
def funcion4(va, vb):
# Crear una lista de ceros con la misma longitud que 'va'
lista_final = [0] * len(va)
# Iterar sobre los indices de las listas.
for i in range(len(va)):
# Asignar el máximo entre los elementos correspondientes de 'va' y 'vb'
lista_final[i] = max(va[i], vb[i])
return lista_final
# Definir los vectores
v1 = [1, 4, 8, 9, 7, 3]
v2 = [4, 5, 7, 8, 2, 1]
# Llamar a la función
resultado = funcion4(v1, v2)
print(resultado)
Estructuras de control o condicionales
Los condicionales permiten ejecutar diferentes bloques de código basados en ciertas condiciones. Son fundamentales para controlar el flujo de un programa. A continuacion se presenta la sintaxis basica:
if condición1:
# Código a ejecutar si condición1 es verdadera
elif condición2:
# Código a ejecutar si condición2 es verdadera
else:
# Código a ejecutar si ninguna de las condiciones anteriores es verdadera
Por ejemplo, supongamos que dada la edad del usuario, queremos identificar si es menor o mayor de edad, o si acaba de cumplir los 18 años.
edad = 20
if edad < 18:
print("Eres menor de edad")
elif edad == 18:
print("Acabas de cumplir 18 años")
else:
print("Eres mayor de edad")
También es posible tener estructuras enlazadas, es decir, condiciones que se deben cumplir al tiempo (and) o que al menos una de las condiciones debe cumplirse (or).
if edad >= 18 and edad <= 65:
print("Eres adulto")
if edad < 18 or edad > 65:
print("Eres menor de edad o adulto mayor")
Para reforzar los aprendido se propone un último ejempo. Se quiere elaborar una función que retornará TRUE si un número específico está dentro de una lista.
# Definir la funcion
def esta_en_lista(numero, lista2):
return numero in lista2
# Definir los parametros
numero = 5
lista_prueba = [3,6,9,6,7,0,1,5]
# Llamar la funcion y sus parametros
esta_en_lista(numero = numero, lista2 = lista_prueba)
Graficas en Python
En Python, crear gráficos y visualizaciones es bastante sencillo gracias a varias bibliotecas. En este caso se utilizará la libreria Matplotlib, una de las bibliotecas de visualización más comunes en Python. Es muy versátil y permite crear una amplia variedad de gráficos.
import matplotlib.pyplot as plt # type: ignore
# Datos de ejemplo
y = [1, 3, 4, 8, 7, 4, 2]
x = [1, 2, 3, 4, 5, 6, 7]
# Crear un gráfico de línea
plt.plot(x, y)
# Añadir título y etiquetas
plt.title('Gráfico de Línea')
plt.xlabel('Eje X')
plt.ylabel('Eje Y')
# Mostrar el gráfico
plt.show()
En este link puedes encontrar mas explicaciones y ejemplos de cómo construir todo tipo de graficas con la libreria Matplotlib: Tutorial Pyplot
Manejo de matrices
Para crear y realizar operaciones sobre matrices en Python utilzaremos la libreria numpy que se abrevia como np.
import numpy as np
Existen diferentes formas para crear matrices en Python. Aqui hay algunos ejemplos:
Se puede crear una matriz a partir de varias listas:
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(matrix)
[[1 2 3]
[4 5 6]
[7 8 9]]
Se puede crear una matriz llena de ceros (esta forma de crear la matriz será de suma utilidad cuando estemos definiendo las cadenas de Markov):
matrix2 = np.zeros((3, 3)) # Matriz 3x3 de ceros
print(matrix2)
[[0. 0. 0.]
[0. 0. 0.]
[0. 0. 0.]]
Crear una matriz identidad (útil para realizar análisis de tiempos)
matrix3 = np.eye(4) # Matriz identidad 4x4
print(matrix3)
[[1. 0. 0. 0.]
[0. 1. 0. 0.]
[0. 0. 1. 0.]
[0. 0. 0. 1.]]
Para acceder a un elemento de una matriz se deben utilizar los índices del respectivo elemento. Se debe tener cuidado ya que los índices en Python empiezan en 0, tal que si, por ejemplo, se quiere acceder a la fila 1 se debe utilizar el 0.
# Accede al elemento en la fila 1, columna 2
elemento = matrix[0, 1]
elemento
2
También se puede extraer filas o columnas de la siguiente manera:
# Extraer la primera fila de 'matrix'.
fila1 = matrix[0,:]
fila1
array([1, 2, 3])
# Extraer la tercera columna de 'matrix'.
columna2 = matrix[:,2]
columna2
array([3, 6, 9])
De igual manera se pueden agregar filas o columnas con la función append. Si se quiere aregar una nueva fila el parámetro axis de la funcion append debe ser igual a 0; si se quiere agregar una nueva columna, axis debe ser igual a 1.
# Nueva fila que se quiere agregar.
nueva_fila = np.array([10,11,12])
# Agregar la nueva fila a la matriz
matrix_con_fila = np.append(matrix, [nueva_fila], axis = 0)
matrix_con_fila
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
# Nueva columna que se quiere agregar.
nueva_columna = np.array([[13], [14], [15]])
# Agregar la nueva columna a la matriz
matrix_con_columna = np.append(matrix, nueva_columna, axis = 1)
matrix_con_columna
array([[ 1, 2, 3, 13],
[ 4, 5, 6, 14],
[ 7, 8, 9, 15]])
Operaciones matriciales
A modo de ejemplo, se crearán dos matrices llenas de números aleatorios que siguen una distribución normal generados por el comando random.normal de la libreria numpy, que tiene como parámetros la media, la desviación estandar y el tamaño de la matriz
A = np.random.normal(loc = 20, scale = 8, size = (6,6))
print(A)
[[10.57592343 17.92167431 22.12330871 38.20083696 2.04917009 16.83960459]
[26.09380602 8.67172598 20.75975553 25.35533819 15.64372048 30.10358743]
[14.39188261 27.57400731 19.62183387 24.63616329 17.16664174 8.41420055]
[22.74912316 18.4647127 31.75504089 15.92631991 19.4332962 28.43490428]
[27.61753947 27.97507546 20.86176904 23.46222247 23.97618136 12.67203208]
[17.40127164 22.1160864 23.48084716 26.28815375 6.72263351 27.1428439 ]]
B = np.random.normal(loc = 10, scale = 3, size = (6,6))
print(B)
[[ 1.94601561 11.86314356 14.41048279 9.20512935 10.09779629 11.52365254]
[ 8.74546308 11.12220969 15.92939796 5.96462469 8.78489055 8.13506776]
[10.94652288 13.05926231 6.65675607 8.04514971 7.75321638 7.00062616]
[ 5.36140743 11.88886116 12.26625887 14.09171993 7.73009502 13.49304627]
[10.71677833 9.92208584 9.92898901 9.95020065 11.38873859 9.01226542]
[14.85279098 13.95810306 11.88936144 13.62482958 10.5896701 9.91085864]]
A continuación, se encuentran algunos comandos de interes que nos permiten realizar operaciones matriciales en Python
Comando |
Explicación |
|---|---|
|
Transpuesta de la matriz A |
|
Suma elemento a elemento de las matrices A y B |
|
Resta elemento a elemento de las matrices A y B |
|
Producto matricial de A por B |
|
Producto elemento a elemento de A por B |
|
Calcula el determinante de la matriz cuadrada A |
|
Calcula la inversa de la matriz cuadrada A |
|
Resuelve el sistema de ecuaciones lineales Ax = b |
|
Calcula los valores y vectores propios de la matriz cuadrada A |
|
Extrae la diagonal principal de la matriz A como un vector |
|
Calcula la suma de los elementos de cada fila de la matriz A |
Cadenas de Markov
El uso de matrices sirve para definir la representación de una cadena de Markov en Python. Por ejemplo, en las cadenas continuas es posible definir la matriz generadora (o de tasas de transición) Q, y en las discretas se define la matriz de probabilidades de transición a un paso P. En Python se utilizará la libreria jmarkov.
¡Ponte a prueba!. Modela la evolución del Índice de calidad del aire (ICA) como una cadena de Markov.
Universidad de los Andes | Vigilada Mineducación. Reconocimiento como Universidad: Decreto 1297 del 30 de mayo de 1964. Reconocimiento personería jurídica: Resolución 28 del 23 de febrero de 1949 Minjusticia. Departamento de Ingeniería Industrial Carrera 1 Este No. 19 A 40 Bogotá, Colombia Tel. (57.1) 3324320 | (57.1) 3394949 Ext. 2880 /2881 http://industrial.uniandes.edu.co
